Wanna bet? If you were offered two bets. Bet A calls for you to put $50 down for a certain win of $100. Bet B calls for you to put $50 down for a 50% chance of winning $200. Which would you choose?
Which bet did you prefer from the two choices? If you chose Bet A you agree with more than 70% of people who are presented with this choice. This experiment and others like it has been carried out thousands of times and the results always favor Bet A as the bet of choice by most people despite the fact that both bets have the same probabilistic outcome. The expected value of Bet A is $50 i.e. a probability of (1.00 x $100) less $50 and the expected value of Bet B is also $50 i.e. (0.50 x $200) – $50.
I believe our natural inclination to avoid what seems to be a risky situation is a barrier to rational decision making and is one of the main reasons people often have difficulty implementing business improvement opportunities that could have a dramatic impact on their bottom line. Daniel Kahneman won a Nobel Prize in economics for demonstrating how this characteristic of human thinking is pervasive. He called the phenomenon, Prospect Theory. His book, Thinking Fast and Slow is one of the most fascinating books I have read in a long time.
He explains Prospect Theory by reference to this diagram. The horizontal axis represents the objective state of a gain or a loss. The vertical axis represents how a person feels about a given gain or a loss i.e. that person’s emotional state. For a given amount of gain e.g. a certain expected net value gain of $50 from Bet A, the positive emotional state is represented by G. However, Bet B presents the possibility of a net loss of $50 but the negative emotional state is not symmetrical to the gain state. Point L is much lower. The top right quadrant of the figure shows the psychological response to positive events and the lower left quadrant shows the response to negative events.
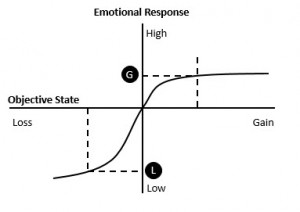 One of the things Kahenaman posits in his theory is that as you get more gain (of something whether it’s ice cream or income) you place a lower emotional value on it. Economists call this diminishing marginal utility. When you look at the lower left quadrant you’ll notice it is also a curve but it starts out much steeper than the gain curve. In essence what Kahenaman is suggesting is that people are naturally risk averse and feel better about a certain gain of, in the case above, of $50 than they do about the possibility of an equivalent loss i.e. negative L is > positive G.
One of the things Kahenaman posits in his theory is that as you get more gain (of something whether it’s ice cream or income) you place a lower emotional value on it. Economists call this diminishing marginal utility. When you look at the lower left quadrant you’ll notice it is also a curve but it starts out much steeper than the gain curve. In essence what Kahenaman is suggesting is that people are naturally risk averse and feel better about a certain gain of, in the case above, of $50 than they do about the possibility of an equivalent loss i.e. negative L is > positive G.
But there’s another interesting point in reflected in the lower negative quadrant. It decreases at a decreasing rate meaning that people place a higher sense of pain on the loss of say their first $50 than on the next. Think about this with another bet.
Suppose you are involved in a double or nothing gamble. You must choose between losing $100 for sure or flip a coin so that if it comes up heads you lose nothing but if it comes up tails you lose $200. What choice would you make.
Interestingly, people who took the conservative choice for the first gamble might be expected to do so with this one as well i.e. accept a sure loss of $100. But that tends not to be the case. As the diagram shows the pain from the loss of the first $100 is greater that the possibility of a loos from another $100. Economists might call this the law of diminishing marginal disutility. This theory seems to explain why many people tend to act irrationally in domains where they are losing e.g. continuing to gamble at a casino in the hope of winning back their losses, holding on to a dying product, retaining dud clients, clinging on to a failing idea or business.
Finally, one of the conclusions that have come out of Kahneman’s research is that people place a negative emotional impact on potential losses which is more than twice the emotional impact they place on potential gains. I have referred to this in another post and in some of my webinars but what it means at a practice level is when you are selling solutions to your clients and prospects the potential payoff needs to be at least twice the expected cost and that includes not just your fee but what the client is expecting to have to commit in addition to your fee. For this reason you should always be looking for at the very least a 3x return and a 10x return is obviously better. When I was in practice that was exactly what we looked for so it’s nice to now learn that there is a solid theoretical foundation for that.
